Introduction
Probably one of the most highly used components on any web page, is the scrollbar. It's far too difficult to fit that much text onto a single page, and it's even harder to do so into the smaller areas SWiSH sites have to work with. So, instead of dividing a large body of text into multiple pages, you can put it into a dynamic text field and add your own scrollbar!
IMPORTANT
Changes in the way SWiSH Max2 handles text objects will either require a change to the actionscript, a change in the export settings, or both. Textfield properties such as scroll, maxscroll, and bottomScroll can be accessed either by using the _text property (eg. myText._text.maxscroll) or by exposing SWF6 properties in the export settings.
So, before continuing with the tutorial, be sure to make this change:
Modify Menu -> Movie Properties -> Export Settings for Movie -> SWF -> Expose SWF6 Properties
Modify Menu -> Movie Properties -> Export Settings for Movie -> SWF -> SWF version to export: SWF6 (or higher)
Setting Up
I am going to try to give specific instructions on re-creating the example shown above. In your own projects, you can obviously use any design style you want - change the positions, sizes, colors, etc. This scrollbar is designed specifically to work with Dynamic text objects. It will not work for scrolling MovieClips or Static Text.
1) Start a new movie (Modify menu | Movie Properties):
Width: 300
Height: 200
2) Modify menu | Movie Properties | Export Settings for Movie
Expose SWF6 Properties
3) Draw a text object on the Stage, then open the Properties panel (it may help to switch to the Selection Tool before changing the object's properties):
Name: textBox
Target: Yes
Font: _sans
Size: 10
Color: Black
Style: Bold
Type: Dynamic
Width: 236
Lines: 12 (disable Auto-size height)
Border: Yes (Black border with white background)
4) Transform Panel
X: 24
Y: 27
O=X: Yes
Transformation point (anchor): Top-Left
Note: Changing an object's _width and/or _height properties on the Transform panel will also change its _xscale and/or _yscale values as well. To maintain 100% scale, use the Reshape panel to alter its unscaled width/unscaled height.
5) Insert a lot of text into this dynamic textfield. If you want, you can generate a couple of paragraphs with the Lorem Ipsum generator.
6) Next, use the rectangle tool and draw a shape on the Stage. Use the Reshape panel to give it these properties:
X: 260
Y: 27
Unscaled Width: 16
Unscaled Height: 16
Transformation Point: Top-Left
O=X: Yes
7) Copy this rectangle shape (Edit Menu -> Copy Object). Then paste it in place (Edit Menu -> Paste in Place).
8) Use the Reshape panel to give it these properties:
X: 260
Y: 43
Unscaled Width: 16
Unscaled Height: 116
Transformation Point: Top-Left
O=X: Yes
9) Use the Properties panel to name it track and select the 'Target' option (you can come back after Step 10 and give the track object a different color, if you'd like).
10) Copy this object and paste it in place. Use the Reshape panel to change its height to 24.
11) Use the Properties panel to change its name to thumb.
12) Next, copy the first rectangle shape (the smaller square) and paste it in place. Use the Reshape panel to change its Y position to 159.
13) Optionally, add an up/down arrow icon to the first and last shapes (I used a bitmap font, but you can use the bezier tool or any dingbat font you want).
Grouping the Pieces
14) Select the first rectangle (smaller square at the top) and any arrow icon you may have placed over it. Group these as a MovieClip (Modify Menu -> Grouping -> Group as MovieClip ). Then name it upScroll on the Properties panel.
15) Repeat the last step for the bottom square and arrow icon, and name it downScroll on the Properties panel.
16) Select the thumb object, group it by itself as a MovieClip and name it slider on the Properties panel.
17) Next, hold down the CTRL key and select both the slider MovieClip and the track object. Group these as a MovieClip and name it scrollBar on the Properties panel.
Scripting the Scrollbar
18) Next, open the scrollBar and slider MovieClips and select the thumb object. Open the Script panel and enter this script:
on (press) {
this.startDragUnlocked(0,0,0,_parent.track._y + (_parent.track._height - this._height));
this.doScroll = setInterval(
function() {
var scrollFactor:Number = _parent._parent.textBox.maxscroll / (_parent.track._height - _height);
_parent._parent.textBox.scroll = Math.ceil(_y * scrollFactor);
updateAfterEvent();
}, 50
);
}
on (release,releaseOutside) {
stopDrag();
clearInterval(doScroll);
}
Explanation: Okay, without getting overly complicated ... setInterval is a slightly more efficient way of writing an onSelfEvent(enterFrame) Event. Instead of happening on every frame (which depends on the frame rate of the movie), the 'function' defined will execute on a set number of milliseconds. In this case, the code fires every 50 milliseconds (although, it's not an exact science). The code calculates the amount of scroll based on comparing the maximum scroll value with the available scroll area (while the user is dragging the slider). When the button is released, the interval is cleared (deleted).
Scripting the Scroll Buttons
19) Open the upScroll MovieClip and select the rectangle shape (should be the bottom object inside the MovieClip). This will be the 'hotspot' for the button. Open the Script panel, and enter the following code:
on (press) {
this.doScroll = setInterval(
function() {
_parent.textBox.scroll -= 1;
var scrollPercent:Number = _parent.textBox.scroll / _parent.textBox.maxscroll;
if (_parent.textBox.scroll == 1) {
_parent.scrollBar.slider._y = 0;
} else if (_parent.textBox.scroll == _parent.textBox.maxscroll){
_parent.scrollBar.slider._y = _parent.scrollBar.track._height - _parent.scrollBar.slider._height;
} else {
_parent.scrollBar.slider._y = (_parent.scrollBar.track._height - _parent.scrollBar.slider._height) * scrollPercent;
}
updateAfterEvent();
}, 50
);
}
on (release,releaseOutside) {
clearInterval(doScroll);
}
Explanation: This code is nearly the same as the slider's code; however, this works a little backward in comparison. The buttons will always scroll exactly 1 line of text on each Interval. At the same time, it takes the current scroll position and compares it with the maximum scroll value and calculates how much to move the slider.
20) Open the downScroll MovieClip and select the rectangle shape (should be the bottom object inside the MovieClip). This will be the 'hotspot' for the button. Open the Script panel, and enter the following code:
on (press) {
this.doScroll = setInterval(
function() {
_parent.textBox.scroll += 1;
var scrollPercent:Number = _parent.textBox.scroll / _parent.textBox.maxscroll;
if (_parent.textBox.scroll == 1) {
_parent.scrollBar.slider._y = 0;
} else if (_parent.textBox.scroll == _parent.textBox.maxscroll){
_parent.scrollBar.slider._y = _parent.scrollBar.track._height - _parent.scrollBar.slider._height;
} else {
_parent.scrollBar.slider._y = (_parent.scrollBar.track._height - _parent.scrollBar.slider._height) * scrollPercent;
}
updateAfterEvent();
}, 50
);
}
on (release,releaseOutside) {
clearInterval(doScroll);
}
Explanation: This code is the same as the upScroll MovieClip's code. The only difference is the first line inside the function - it scrolls +1 rather than -1.
Note: If you want either of those buttons (upScroll or downScroll) to scroll through the text faster or slower, you can adjust the "50" at the bottom of the SetInterval function. A lower number will scroll faster, while a higher number will scroll slower
At this point, you should have a fully functioning scrollbar component. You can take it a few steps further if you'd like; I just wanted to focus on the basics. You could make the height of the slider more dynamic by comparing the total lines of text and inversely altering the height of the slider (more text = smaller slider, and vice versa). You could also add script to the track object to make it act as a button, too (a "scroll here" effect). There are countless possibilities. This is by no means the only way to create a scrollbar component ... it's just the one I decided to write about =)
Jumat, 23 Mei 2008
Linking to Other Web Pages
Introduction
A short tutorial showing how to create hyperlinks to other web pages (URLs). The same method can be used to create links to external files - such as ZIP, DOC, PDF, MP3, etc.
Important
There can be problems testing external links locally (from your computer). One of the features of the latest Flash Player is heightened security. Basically, when you install it, you need to visit Adobe/Macromedia's online settings manager to choose and apply your settings. This should only need to be done once - on any computer you use for development and testing.
This thread in our forums covers the topic in some detail and provides links to the settings manager:
http://forums.swishzone.com/index.php?showtopic=26790
When creating links to external files such as PDF documents, keep in mind that the file will most likely open in the default application set on the viewer's computer. In the case of PDF files, creating a link to it will usually open the file in the browser with Acrobat Reader. If you link to an MP3 file, it will probably open in the viewer's media player (WinAmp, Windows Media Player, Quicktime, etc.) If you want to allow the user to save the file to their computer, it is recommended to ZIP (or RAR) the file and link to that instead.
Setting Up
The actionscript for hyperlinks is very simple. I'll show how to do it using point-and-click methods with the Assist Pane on the Script panel.
You can turn any shape, image, text, object, or MovieClip into a hyperlink. So, open a new file in SWiSH Max2 and draw a rectangle shape on the Layout. Select that shape and open the Script panel.
1) Add Script -> Events -> Button -> on (release)
2) Add Script -> Browser/Network -> getURL(...)
3) On the Assist Pane, type in the web page you want to open in the URL field.
4) In the Window field, you can select (or type in) a target frame. The default options _self and _blank refer to the browser window itself. If you select _self, it will open the URL in the same browser window. If you select _blank, it will open a new browser window and go to the URL provided. The options _top and _parent refer to Framesets (HTML Frames). If you are using a frameset and want to open a URL in a specific frame, you will need to know the exact name of that frame (written in the HTML frameset code). Whatever name is in the HTML is what you would type into the Window field.
You should end up with a script similar to this:
on (release)
{
getURL("http://www.example.com", "_blank");
}
A short tutorial showing how to create hyperlinks to other web pages (URLs). The same method can be used to create links to external files - such as ZIP, DOC, PDF, MP3, etc.
Important
There can be problems testing external links locally (from your computer). One of the features of the latest Flash Player is heightened security. Basically, when you install it, you need to visit Adobe/Macromedia's online settings manager to choose and apply your settings. This should only need to be done once - on any computer you use for development and testing.
This thread in our forums covers the topic in some detail and provides links to the settings manager:
http://forums.swishzone.com/index.php?showtopic=26790
When creating links to external files such as PDF documents, keep in mind that the file will most likely open in the default application set on the viewer's computer. In the case of PDF files, creating a link to it will usually open the file in the browser with Acrobat Reader. If you link to an MP3 file, it will probably open in the viewer's media player (WinAmp, Windows Media Player, Quicktime, etc.) If you want to allow the user to save the file to their computer, it is recommended to ZIP (or RAR) the file and link to that instead.
Setting Up
The actionscript for hyperlinks is very simple. I'll show how to do it using point-and-click methods with the Assist Pane on the Script panel.
You can turn any shape, image, text, object, or MovieClip into a hyperlink. So, open a new file in SWiSH Max2 and draw a rectangle shape on the Layout. Select that shape and open the Script panel.
1) Add Script -> Events -> Button -> on (release)
2) Add Script -> Browser/Network -> getURL(...)
3) On the Assist Pane, type in the web page you want to open in the URL field.
4) In the Window field, you can select (or type in) a target frame. The default options _self and _blank refer to the browser window itself. If you select _self, it will open the URL in the same browser window. If you select _blank, it will open a new browser window and go to the URL provided. The options _top and _parent refer to Framesets (HTML Frames). If you are using a frameset and want to open a URL in a specific frame, you will need to know the exact name of that frame (written in the HTML frameset code). Whatever name is in the HTML is what you would type into the Window field.
You should end up with a script similar to this:
on (release)
{
getURL("http://www.example.com", "_blank");
}
CTL
Contextual Teaching and Learning (CTL) helps us relate subject matter content to real world situations and motivate students to make connections between knowledge and its applications to their lives as family members, citizens, and workers and engage in the hard work that learning requires. Contextual teaching and learning strategies:
[1] Problem-based.
[2] Using multiple contexts.
[3] Drawing upon student diversity.
[4] Supporting self-regulated learning.
[5] Using interdependent learning groups.
[6] Employing authentic assessment.
[1] Problem-based.
[2] Using multiple contexts.
[3] Drawing upon student diversity.
[4] Supporting self-regulated learning.
[5] Using interdependent learning groups.
[6] Employing authentic assessment.
Inquiry Based Lerning
"Inquiry" is defined as "a seeking for truth, information, or knowledge -- seeking information by questioning." Individuals carry on the process of inquiry from the time they are born until they die. This is true even though they might not reflect upon the process. Infants begin to make sense of the world by inquiring. From birth, babies observe faces that come near, they grasp objects, they put things in their mouths, and they turn toward voices. The process of inquiring begins with gathering information and data through applying the human senses -- seeing, hearing, touching, tasting, and smelling.
A Context for Inquiry
Unfortunately, our traditional educational system has worked in a way that discourages the natural process of inquiry. Students become less prone to ask questions as they move through the grade levels. In traditional schools, students learn not to ask too many questions, instead to listen and repeat the expected answers.
Some of the discouragement of our natural inquiry process may come from a lack of understanding about the deeper nature of inquiry-based learning. There is even a tendency to view it as "fluff" learning. Effective inquiry is more than just asking questions. A complex process is involved when individuals attempt to convert information and data into useful knowledge. Useful application of inquiry learning involves several factors: a context for questions, a framework for questions, a focus for questions, and different levels of questions. Well-designed inquiry learning produces knowledge formation that can be widely applied.
A Context for Inquiry
Unfortunately, our traditional educational system has worked in a way that discourages the natural process of inquiry. Students become less prone to ask questions as they move through the grade levels. In traditional schools, students learn not to ask too many questions, instead to listen and repeat the expected answers.
Some of the discouragement of our natural inquiry process may come from a lack of understanding about the deeper nature of inquiry-based learning. There is even a tendency to view it as "fluff" learning. Effective inquiry is more than just asking questions. A complex process is involved when individuals attempt to convert information and data into useful knowledge. Useful application of inquiry learning involves several factors: a context for questions, a framework for questions, a focus for questions, and different levels of questions. Well-designed inquiry learning produces knowledge formation that can be widely applied.
Problem Based Learning
Problem-based learning (PBL) is a student-centered instructional strategy in which students collaboratively solve problems and reflect on their experiences. It was pioneered and used extensively at McMaster University, Hamilton, Ontario, Canada. Characteristics of PBL are:
[1] Learning is driven by challenging, open-ended problems.
[2] Students work in small collaborative groups.
[3] Teachers take on the role as "facilitators" of learning.
Accordingly, students are encouraged to take responsibility for their group and organize and direct the learning process with support from a tutor or instructor. Advocates of PBL claim it can be used to enhance content knowledge and foster the development of communication, problem-solving, and self-directed learning skill.
[1] Learning is driven by challenging, open-ended problems.
[2] Students work in small collaborative groups.
[3] Teachers take on the role as "facilitators" of learning.
Accordingly, students are encouraged to take responsibility for their group and organize and direct the learning process with support from a tutor or instructor. Advocates of PBL claim it can be used to enhance content knowledge and foster the development of communication, problem-solving, and self-directed learning skill.
Team Game Tournament Instructions
This learning activity appeals to many different types of learner including the cooperative and the competitive learner.
Step1 Divide the class into teams of four or five. A class of 29 would have 5 teams of 5 and one team of 4.
Step 2 Distribute the Practice version of the test to each student and instruct them to answer the questions cooperatively as a team, ensuring that all team members understand how each answer was obtained. The intention is to lift the overall team performance.
Step 3 Display a copy of the answers on the OHP or data projector and get each team to check their answers and resolve any issues with their answers.
Step 4 Ask the students to sort there team on the basis of their understanding of the topic from very good understanding (A students) to poor understanding (E students). The team of 4 students will only have A to D students.
Step 5 Regroup and seat all of the A students in one area of the room, B students in another area etc.
Step 6 Give out the Test version questions to each student and instruct them to individually answer the questions under formal test conditions.
Step 7 Display a copy of the answers on the OHP or data projector and get each student to mark their answers and then to rank themselves amongst the group of students the y are grouped with. That is, the A students will rank themselves from best to worst score. The student with the best score is given a score of 5` points while the student with the lowest score is given a score of 1 point. Students with equal scores receive the same number of points (e.g. the points distribution could be 5, 4, 4, 4, 1 if three students have the same score). If there are only four students in a group, the scores will range from 5 to 2 points.
Step 8 The students recombine into their original teams and total their scores with the largest score winning. Any team with less than 5 students adds the average grade for the team to their score.
Step1 Divide the class into teams of four or five. A class of 29 would have 5 teams of 5 and one team of 4.
Step 2 Distribute the Practice version of the test to each student and instruct them to answer the questions cooperatively as a team, ensuring that all team members understand how each answer was obtained. The intention is to lift the overall team performance.
Step 3 Display a copy of the answers on the OHP or data projector and get each team to check their answers and resolve any issues with their answers.
Step 4 Ask the students to sort there team on the basis of their understanding of the topic from very good understanding (A students) to poor understanding (E students). The team of 4 students will only have A to D students.
Step 5 Regroup and seat all of the A students in one area of the room, B students in another area etc.
Step 6 Give out the Test version questions to each student and instruct them to individually answer the questions under formal test conditions.
Step 7 Display a copy of the answers on the OHP or data projector and get each student to mark their answers and then to rank themselves amongst the group of students the y are grouped with. That is, the A students will rank themselves from best to worst score. The student with the best score is given a score of 5` points while the student with the lowest score is given a score of 1 point. Students with equal scores receive the same number of points (e.g. the points distribution could be 5, 4, 4, 4, 1 if three students have the same score). If there are only four students in a group, the scores will range from 5 to 2 points.
Step 8 The students recombine into their original teams and total their scores with the largest score winning. Any team with less than 5 students adds the average grade for the team to their score.
Jigsaw in 10 Easy Steps
The jigsaw classrom is very simple to use. If you're a teacher, just follow these steps:
[1] Divide students into 5- or 6-person jigsaw groups. The groups should be diverse in terms of gender, ethnicity, race, and ability.
[2] Appoint one student from each group as the leader. Initially, this person should be the most mature student in the group.
[3] Divide the day's lesson into 5-6 segments. For example, if you want history students to learn about Eleanor Roosevelt, you might divide a short biography of her into stand-alone segments on: (1) Her childhood, (2) Her family life with Franklin and their children, (3) Her life after Franklin contracted polio, (4) Her work in the White House as First Lady, and (5) Her life and work after Franklin's death.
[4] Assign each student to learn one segment, making sure students have direct access only to their own segment.
[5] Give students time to read over their segment at least twice and become familiar with it. There is no need for them to memorize it.
[6] Form temporary "expert groups" by having one student from each jigsaw group join other students assigned to the same segment. Give students in these expert groups time to discuss the main points of their segment and to rehearse the presentations they will make to their jigsaw group.
[7] Bring the students back into their jigsaw groups.
[8] Ask each student to present her or his segment to the group. Encourage others in the group to ask questions for clarification.
[8] Float from group to group, observing the process. If any group is having trouble (e.g., a member is dominating or disruptive), make an appropriate intervention. Eventually, it's best for the group leader to handle this task. Leaders can be trained by whispering an instruction on how to intervene, until the leader gets the hang of it.
[10] At the end of the session, give a quiz on the material so that students quickly come to realize that these sessions are not just fun and games but really count.
[1] Divide students into 5- or 6-person jigsaw groups. The groups should be diverse in terms of gender, ethnicity, race, and ability.
[2] Appoint one student from each group as the leader. Initially, this person should be the most mature student in the group.
[3] Divide the day's lesson into 5-6 segments. For example, if you want history students to learn about Eleanor Roosevelt, you might divide a short biography of her into stand-alone segments on: (1) Her childhood, (2) Her family life with Franklin and their children, (3) Her life after Franklin contracted polio, (4) Her work in the White House as First Lady, and (5) Her life and work after Franklin's death.
[4] Assign each student to learn one segment, making sure students have direct access only to their own segment.
[5] Give students time to read over their segment at least twice and become familiar with it. There is no need for them to memorize it.
[6] Form temporary "expert groups" by having one student from each jigsaw group join other students assigned to the same segment. Give students in these expert groups time to discuss the main points of their segment and to rehearse the presentations they will make to their jigsaw group.
[7] Bring the students back into their jigsaw groups.
[8] Ask each student to present her or his segment to the group. Encourage others in the group to ask questions for clarification.
[8] Float from group to group, observing the process. If any group is having trouble (e.g., a member is dominating or disruptive), make an appropriate intervention. Eventually, it's best for the group leader to handle this task. Leaders can be trained by whispering an instruction on how to intervene, until the leader gets the hang of it.
[10] At the end of the session, give a quiz on the material so that students quickly come to realize that these sessions are not just fun and games but really count.
RME
Realistic Mathematics Education, or RME, is the Dutch answer to the world-wide felt need to reform the teaching and learning of mathematics. The roots of the Dutch reform movement go back to the early seventies when the first ideas for RME were conceptualized. It was a reaction to both the American "New Math" movement that was likely to flood our country in those days, and to the then prevailing Dutch approach to mathematics education, which often is labeled as "mechanistic mathematics education."
Since the early days of RME much development work connected to developmental research has been carried out. If anything is to be learned from the Dutch history of the reform of mathematics education, it is that such a reform takes time. This sounds like a superfluous statement, but it is not. Again and again, too optimistic thoughts are heard about educational innovations. The following statement indicates how we think about this: The development of RME is thirty years old now, and we still consider it as "work under construction."
That we see it in this way, however, has not only to do with the fact that until now the struggle against the mechanistic approach to mathematics education has not been completely conquered— especially in classroom practice much work still has to be done in this respect. More determining for the continuing development of RME is its own character. It is inherent to RME, with its founding idea of mathematics as a human activity, that it can never be considered a fixed and finished theory of mathematics education.
Since the early days of RME much development work connected to developmental research has been carried out. If anything is to be learned from the Dutch history of the reform of mathematics education, it is that such a reform takes time. This sounds like a superfluous statement, but it is not. Again and again, too optimistic thoughts are heard about educational innovations. The following statement indicates how we think about this: The development of RME is thirty years old now, and we still consider it as "work under construction."
That we see it in this way, however, has not only to do with the fact that until now the struggle against the mechanistic approach to mathematics education has not been completely conquered— especially in classroom practice much work still has to be done in this respect. More determining for the continuing development of RME is its own character. It is inherent to RME, with its founding idea of mathematics as a human activity, that it can never be considered a fixed and finished theory of mathematics education.
Integral
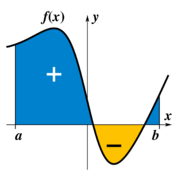
The term "integral" may also refer to the notion of antiderivative, a function F whose derivative is the given function f. In this case it is called an indefinite integral, while the integrals discussed in this article are termed definite integrals. Some authors maintain a distinction between antiderivatives and indefinite integrals
History
Pre-calculus integration
Integration can be traced as far back as ancient Egypt, circa 1800 BC, with the Moscow Mathematical Papyrus demonstrating knowledge of a formula for the volume of a pyramidal frustum. The first documented systematic technique capable of determining integrals is the method of exhaustion of Eudoxus (circa 370 BC), which sought to find areas and volumes by breaking them up into an infinite number of shapes for which the area or volume was known. This method was further developed and employed by Archimedes and used to calculate areas for parabolas and an approximation to the area of a circle. Similar methods were independently developed in China around the 3rd Century AD by Liu Hui, who used it to find the area of the circle. This method was later used by Zu Chongzhi to find the volume of a sphere. Some ideas of integral calculus are found in the Siddhanta Shiromani, a 12th century astronomy text by Indian mathematician Bhāskara II.
Significant advances on techniques such as the method of exhaustion did not begin to appear until the 16th century AD. At this time the work of Cavalieri with his method of indivisibles, and work by Fermat, began to lay the foundations of modern calculus. Further steps were made in the early 17th century by Barrow and Torricelli, who provided the first hints of a connection between integration and differentiation.
Symilarity
Two geometrical objects are called similar if one is congruent to the result of a uniform scaling (enlarging or shrinking) of the other. One can be obtained from the other by uniformly "stretching", possibly with additional rotation, i.e., both have the same shape, or additionally the mirror image is taken, i.e., one has the same shape as the mirror image of the other. For example, all circles are similar to each other, all squares are similar to each other, and all parabolas are similar to each other. On the other hand, ellipses are not all similar to each other, nor are hyperbolas all similar to each other. Two triangles are similar if and only if they have the same three angles, the so-called "AAA" condition. However, since the sum of the interior angles in a triangle is fixed in an euclidean plane, as long as two angles are the same, all three are, called "AA
Type of Triangle 2
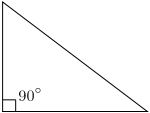
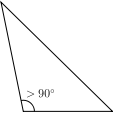
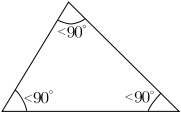
Triangles can also be classified according to their internal angles, described below using degrees of arc:
[1] A right triangle (or right-angled triangle, formerly called a rectangled triangle) has one 90° internal angle (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side in the right triangle. The other two sides are the legs or catheti (singular: cathetus) of the triangle.
[2] An oblique triangle has no internal angle equal to 90°.
[3] An obtuse triangle is an oblique triangle with one internal angle larger than 90° (an obtuse angle).
An acute triangle is an oblique triangle with internal angles all smaller than 90° (three acute angles). An equilateral triangle is an acute triangle, but not all acute triangles are equilateral triangles
Type of Triangel 1
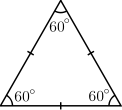
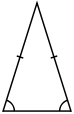
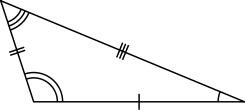
Triangles can be classified according to the relative lengths of their sides:
[1] In an equilateral triangle, all sides are of equal length. An equilateral triangle is also an equiangular polygon, i.e. all its internal angles are equal—namely, 60°; it is a regular polygon.
[2] In an isosceles triangle, two sides are of equal length (originally and conventionally limited to exactly two). An isosceles triangle also has two equal angles: the angles opposite the two equal sides.
[3] In a scalene triangle, all sides have different lengths. The internal angles in a scalene triangle are all different.
Triangle
Trapezoid
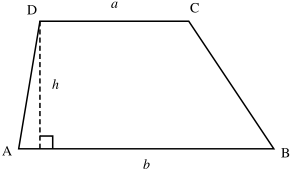
A trapezoid (in North America) or a trapezium (in Britain and elsewhere) is a quadrilateral, which is defined as a closed shape with four linear sides, that has one pair of parallel lines for sides. Some authors [1] define it as a quadrilateral having exactly one pair of parallel sides, so as to exclude parallelograms, which otherwise would be regarded as a special type of trapezoid, but most mathematicians use the inclusive definition.
The area formula is as follows:
A = h x ((a+b)/2)
Rhombus
Circles
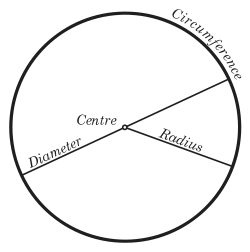
Circles are simple shapes of Euclidean geometry. A circle consists of those points in a plane which are at a constant distance, called the radius, from a fixed point, called the center.
The circumference of a square whose sides have length t is
C = 2 x pi x r, pi = 3.1415926535
And the area is
A = pi x r^2, pi = 3.1415926535.
Parallelogram
Square
Definition of Julia Set

Definition 2.4.1. Let f: X X is an analytic self-map of a Riemann surface X. We will assume that X is the Riemann sphere, the complex plane, or the once-punctured complex plane, as the other cases do not give rise to interesting dynamics. (Such maps are completely classified.)
It will consider f as a discrete dynamical system on the phase space X, so we are interested in the behavior of the iterates fn of f (that is, the n-fold compositions of f with itself).
The Fatou set of f consists of all points z X such that the family of iterates , forms a normal family in the sense of Montel when restricted to some open neighborhood of z. The Julia set of f is the complement of the Fatou set in X.
Criteria for PBL
According to the Autodesk Foundation, "PBL is at the heart of good instruction because it brings together intellectual inquiry, rigorous real-world standards, and student engagement in relevant and meaningful work." Well-crafted projects:
• Engage and build on student interests and passions,
• Provide a meaningful and authentic context for learning,
• Immerse students in complex, real-world problems/investigations without a edetermined solution,
• Allow students to take the lead, making critical choices and decisions,
• Connect students with community resources and experts,
• Require students to develop and demonstrate essential skills and knowledge,
• Draw on multiple disciplines to solve problems and deepen understanding,
• Build in opportunities for reflection and self-assessment,
• Result in useful products that demonstrate what students have learned, and
• Culminate in exhibitions or presentations to an authentic audience.
• Engage and build on student interests and passions,
• Provide a meaningful and authentic context for learning,
• Immerse students in complex, real-world problems/investigations without a edetermined solution,
• Allow students to take the lead, making critical choices and decisions,
• Connect students with community resources and experts,
• Require students to develop and demonstrate essential skills and knowledge,
• Draw on multiple disciplines to solve problems and deepen understanding,
• Build in opportunities for reflection and self-assessment,
• Result in useful products that demonstrate what students have learned, and
• Culminate in exhibitions or presentations to an authentic audience.
Project Based Learning
Project-based learning (PBL) is a model that organizes learning around projects.According to the definitions found in PBL handbooks for teachers, projects are complex tasks,based on challenging questions or problems, that involve students in design, problem-solving, decision making, or investigative activities; give students the opportunity to work relatively autonomously over extended periods of time; and culminate in realistic products or presentations (Jones, Rasmussen, & Moffitt, 1997; Thomas, Mergendoller, & Michaelson, 1999). Other defining features found in the literature include authentic content, authentic assessment, teacher facilitation but not direction, explicit educational goals, (Moursund, 1999), cooperative learning, reflection, and incorporation of adult skills (Diehl, Grobe, Lopez, & Cabral, 1999). To these features, particular models of PBL add a number of unique features. Definitions of "project-based instruction" include features relating to the use of an authentic ("driving") question, a community of inquiry, and the use of cognitive (technology-based) tools (Krajcik, Blumenfeld, Marx, & Soloway, 1994; Marx, Blumenfeld, Krajcik, Blunk, Crawford, Kelly, & Meyer, 1994 ); and "Expeditionary Learning" adds features of comprehensive school improvement, community service, and multidisciplinary themes (Expeditionary Learning Outward Bound, 1999a).
Mathematics and Batik
Batik is one of original Indonesian cultural art. Combining with the beautifulness of mathematics, there are innovative motifs of batik based on mathematics. The Julia Set graph is one that shows how beautiful mathematics. By using Maple 7TM, the Julia Set graph can be drawn as new innovative batik motifs. The result of this innovative batik motif will be given to the Kampoeng Batik, a place to develop batik in Wiradesa, Pekalongan. In this paper, it will be explained how to make batik motif based on Julia Set Graph.
(Ardhi Prabowo, Laely R.A., M. Jazilun Ni'am, Ali Murtandho)
(Ardhi Prabowo, Laely R.A., M. Jazilun Ni'am, Ali Murtandho)
Langganan:
Postingan (Atom)





