Integral

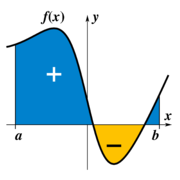
The term "integral" may also refer to the notion of antiderivative, a function F whose derivative is the given function f. In this case it is called an indefinite integral, while the integrals discussed in this article are termed definite integrals. Some authors maintain a distinction between antiderivatives and indefinite integrals

History

Pre-calculus integration

Integration can be traced as far back as ancient Egypt, circa 1800 BC, with the Moscow Mathematical Papyrus demonstrating knowledge of a formula for the volume of a pyramidal frustum. The first documented systematic technique capable of determining integrals is the method of exhaustion of Eudoxus (circa 370 BC), which sought to find areas and volumes by breaking them up into an infinite number of shapes for which the area or volume was known. This method was further developed and employed by Archimedes and used to calculate areas for parabolas and an approximation to the area of a circle. Similar methods were independently developed in China around the 3rd Century AD by Liu Hui, who used it to find the area of the circle. This method was later used by Zu Chongzhi to find the volume of a sphere. Some ideas of integral calculus are found in the Siddhanta Shiromani, a 12th century astronomy text by Indian mathematician Bhāskara II.

Significant advances on techniques such as the method of exhaustion did not begin to appear until the 16th century AD. At this time the work of Cavalieri with his method of indivisibles, and work by Fermat, began to lay the foundations of modern calculus. Further steps were made in the early 17th century by Barrow and Torricelli, who provided the first hints of a connection between integration and differentiation.